Altitude Control Design and Performance Validation for Unmanned Aerial Vehicle with a Single Ducted-Fan
Abstract
In this paper, the authors propose a novel control method for altitude control of aerial vehicle by extending the sliding mode law with fuzzy law and feedback control (F-SMFC). The key issue in the sliding mode control method is to suppress the chattering phenomenon. By providing a new control strategy, the solutions of the problems such as governing the chattering phenomenon and arbitrarily exploiting the numeric control by the fuzzy law were obtained. Also, it was shown that the F-SMFC method can cope with the unknown physical parameter of the system. The proposed control method was applied to the altitude control of the single ducted-fan unmanned aerial vehicle (UAV). Both simulation and experimental results were demonstrated to validate effectiveness and satisfactory performances of the proposed controller.
Keywords:
Altitude control, Fuzzy control, F-SMFC, Sliding mode control, Ducted-Fan UAV1. Introduction
By the Fast development of automatic flight cybernetic technologies, the vertical take-off and landing technology of unmanned aerial vehicles (VTOL UAVs) has been developed gradually that dominate the military field and humanitarian relief forces. Because the VTOL UAVs possess VTOL ability, high maneuverability during vertical and horizontal flights and high efficiency in level flights. The strong abilities have been investigated by many researches for a longtime.1-5) In a turn of VTOL UAVs, ducted-fan unmanned aerial vehicle (DUAV) technology has gradually grown based on the combination of its properties.
Typically, the motion control principle of DUAV is similar to the missile motion in longitudinal and lateral flights. At this moment, the source of lift and aerodynamics of DUAV is solely coming from the thrust like helicopters or multi rotor copters. On the contrary, the effects of aerodynamic on DUAV are similar to the aircraft.6-8) Hence, the DUAV highlights the need to exploit the outstanding properties of the missile, helicopter and aircraft by providing superior performance in the research areas. To overcome these intrinsic limitations, a simple configuration of the flight dynamic modeling of DUAV has been researched and presented in recent years.9-11) Besides, the design of an unmaned aerial vehicle was studied by Muehlebach et al.12) by using the electric ducted fans as the propulsion system. A cascaded control method was used for controling two more propulsion systems.
Hence, it was quite complicated to implement. Omar et al. developed a fuzzy logic controller under the configuration of ducted-fan VTOL UAV to automate the transition maneuver.13) It is worth noting that using fuzzy logic law generates the smooth transition flight in the DUAV system. However, only fuzzy logic controller dose not clearly demonstrate the effectiveness of altitude control of DUAV system. By many attempts, such as Naldi et al. discussed a validation of nonlinear control law for the ducted-fan miniature aerial vehicle. It was shown that the dynamics of the aircraft tracked robustly the arbitrary lateral and longitudinal references.14)
In contrast, the application of nonlinear control law methods was much less mature and had some fundamental disadvantages. Few of the disadvantages were the aerodynamic forces and moments which acted on UAV including several elements and variables. And, other parts are constants such as body force, buoyancy and so on, which needed to be properly elaborated. Another area of current interest is the several approaches in sliding mode control (SMC) technology that were collected and reported by Sarah.15,16) After decades of research, the SMC strategy provided superior performance design methodologies such as output feedback SMC, fuzzy SMC and super-twisting algorithm etc, which made more advanced control performance.17,18)
Notably, the SMC strategy is designed based on the Lyapunov theory. It is evident that the SMC has the properties of finite time convergence and robustness against uncertain internal and external dynamic system characteristics.
Autonomous flying topics were strong to focus on developing and researching in recent years as mentioned above. However, the research on autonomous taking off and landing with control allocation for DUAV has seen little attention (see Fig. 1). Therefore, from both theoretical and technical challenges of ducted-fan UAV and advantages of SMC analysis respects, an altitude motion of DUAV needs to be properly elaborated. Based on these facts, this article proposes a new approach of SMC method by combining the fuzzy-sliding mode-feedback control (F-SMFC) to solve the problems such as governing the chattering phenomenon and arbitrarily exploiting the numeric control by the fuzzy law. More interestingly, the advantages of this method are not affected by the physical parameters, and the states reach the equilibrium point in a shorter time. To demonstrate the effectiveness and satisfactory performance, the comparisons of the performance of Ziegler-Nichols tuning PID, classical sliding mode control (SMC) and the proposed controller (F-SMFC) will be given by simulation and experiment. Finally, the root mean square error method has been used to evaluate the tracking performances. Then, the contributions of this paper are emphasized as follows :
•Fabrication of a scaled model and modeling of DUAV
•Design of Ziegler-Nichols tuning PID and classical sliding mode control
•Design of novel controller based on fuzzy-sliding mode-feedback scheme
•Stability analysis
•Comparison study for Ziegler-Nichols tuning PID, classical SMC and F-SMFC
•Simulation and experiment
Then, this article is organized as follows.
Section 2 discusses the modeling of the DUAV system. Section 3 analytically presents the design of Ziegler-Nichols tuning PID, classical SMC and F-SMFC for controlling altitude of the system, and provides the convergence and stability condition by Lyapunov theory. The simulation results of the theoretical findings are presented in section 4. The experiment results of the DUAV system are illustrated in section 5. In section 6, conclusions will be drawn.
2. DUAV modeling
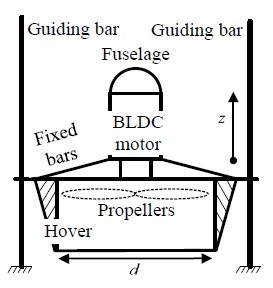
The controlled DUAV shown in Fig. 2 consists of two main different subsystems, fuselage and hover. The brushless DC motor (BLDC) has the main role for generating the necessary main thrust to counteract the gravitation of DUAV.
The fuselage contains all the avionics, sensor and hardware, etc. The fuselage and hover subsystem are assisted by the bars for stable up and down. Obviously, identification and tuning of the DUAV parameters were done by following general method with experiment and simulation. The experimental apparatus with controlled plant and sensing systems are shown in Fig. 3. The precise specifications of them are summarized in Table 5.
Mathematical model of DUAV can be presented as a second order system as follow:
| (1) |
where z is the altitude of DUAV and τu* is the control input to the actuator. And, we define b=aM/mg and c=bM/mg. Where aM and bM are the coefficient parameters of BLDC motor. g is gravity acceleration, d is inside diameter of hover and m is the mass of the system.
Then, the identified parameter values shown in Eq. (1) are obtained as b=0.024674, c=-0.442705. And the function presenting an inertia acceleration is defined as
| (2) |
where [N] is nominal value of friction force. And, the d(t) is
| (3) |
where dsys(t) is the disturbance and ds(t)is the sensing noise.
Remark 17) We assume that the slipstream axis is coincident with the fan axis. Assumption on this slipstream model, no account is taken for the possibility of mixing the slipstream with other external duct flows. Also, there is no cross-wind in the system.
3. Controller design
The authors design three kinds of controller for control performance evaluation.
3.1 Conventional sliding mode control
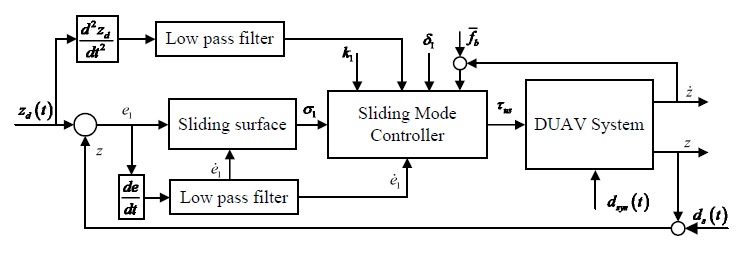
In the first level, as depicted on Fig. 4 and Eq. (1), the controller is disposed radially around sliding mode law (SMC). The stability of SMC is demonstrated with Lyapunov stability theory. Based on these results, the authors design a control system for controlling DUAV altitude motion by developing the fuzzy-sliding mode-feedback (F-SMFC). For this, let us define a position tracking error and sliding surface as follows :
| (4) |
| (5) |
where zd is a desired altitude of the DUAV system and k1 is the positive gain.
Remark 215) The gain k1 is chosen such that is Hurwitz polynomial. Then e1(t)→0 when σ1(t)=0 with t→∞. The time derivative of Eq. (5) gives
| (6) |
From Eq. (1), Eq. (4) and Eq. (6), the Eq. (7) is obtained with Eq. (8) which is the sliding surface.
| (7) |
| (8) |
Then, the control law on the sliding mode control is interpreted as :
| (9) |
where δ1 is a positive gain. And, the function sign(·) is defined as follows :
| (10) |
Proof Consider a following Lyapunov candidate :
| (11) |
The control signal τus is chosen so that σ1(t)→0 and e1(t)→0 with the condition :
| (12) |
By taking the time derivative of the Lyapunov candidate Eq. (11), the following condition is obtained.
| (13) |
From this result, the stability of system with the control law Eq. (9) is verified. Then, a designed conventional sliding mode control scheme is shown in Fig. 4.
3.2 PID control method
In more practical terms, the authors design a PID controller based on Ziegler-Nichols tuning method.19) The PID control gains are depicted on the Table 1. In the Table 1, L is desired time delay of the system, T is desired time response of the system.
3.3 Proposed controller : Fuzzy-sliding mode-feedback control
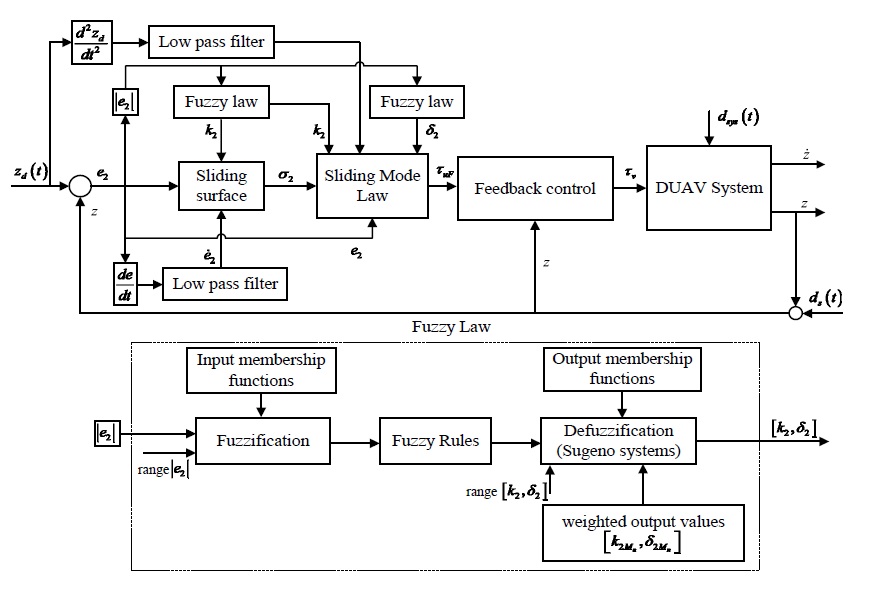
In this paper, the authors design a novel sliding mode control by combining fuzzy law to enhance the control performance.
For this purpose, the proposed control (F-SMFC) scheme requires a detailed knowledge. The block diagram of the proposed controller is shown in Fig. 5.
| (14) |
And denote the sliding surface as :
| (16) |
Remark 315) The coefficients k2 is defined so that is Hurwitz polynomial. Then, e2(t)→0 when σ2(t)=0 at △(s)=0 with t→∞. Taking the time derivative of Eq. (15) gives :
| (17) |
The sliding mode control law is depicted as
| (18) |
And, the function sign(·) is defined as :
| (19) |
where δ2 and ξ2 are positive values.
The control signal of the sliding mode control law Eq. (18) governs the chattering phenomenon by Eq. (19) and the states reach to the equilibrium point in shorter time.
Proof Set a Lyapunov candidate as :
| (20) |
The control τuF preserves that σ2(t)→0 and e2(t)→0 with the following condition.
| (21) |
Substituting Eq. (17) and Eq. (21) into the time derivative of the Lyapunov candidate Eq. (20) yields :
| (22) |
such that the defined condition is satisfied.
Here, let us redefine the system Eq. (1) to follow the feedback control law :
| (23) |
Substituting Eq. (1) and Eq. (16) into Eq. (21), the control of system can be obtained as follows :
| (24) |
Obviously, the advantage of the control rule of Eq. (24) based on sliding mode and feedback law describes that it is not affected by the physical parameters of the system. Furthermore, we aim to manage the amplitude and oscillation on altitude tracking control. For this, a cascade control is carried out to construct the variable inputs by using the advantage of fuzzy law. The control rule presented in Eq. (24) is served by two main gains, δ2 and k2. Herein, the gain k2 is indexed as the oscillation error on the altitude tracking.
Hence, the behavior of the output gain k2 is regulated by the characteristic of the input variable which is the altitude error (Eq. (14)). Likewise, the gain δ2 is indexed as the amplitude around sliding surface. So, we manage the behavior of the output gain δ2 on the convergent equilibrium point. Based on the definitions, let us define the range of δ2 and k2 as follow :
| (25) |
| (26) |
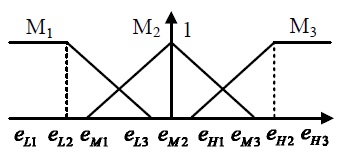
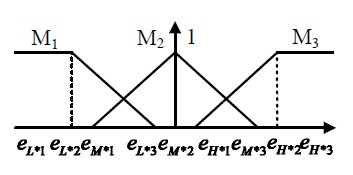
The membership functions of fuzzy input variables are shown in Fig. 6 and Fig. 7. The numbers of the fuzzy sets eHi,eLi,eMi(i=1,2,3) can be obtained by simulation and experiment. Based on the membership functions and fuzzy sets, the fuzzy rules for selecting the control gains are illustrated in Table 2. If the altitude error ei(t)∈Mi, then the output of fuzzy sets is taken as μMi(t)∈[0 1]. Finally, the output variables (δ2,k2) are defuzzified by Sugeno system as follows20) :
| (27) |
| (28) |
where μMn(t)(n=1,2,3) is the numeric indicator of output fuzzy sets Mi, δMn and kMn are numeric weights of δ2 and k2, respectively.
4. Simulation
The initial values are to be defined to initialize the simulation condition for all control systems.
Those are sliding mode control (SMC), fuzzy-sliding mode-feedback control (F-SMFC) and PID Ziegler-Nichols tuning method. And, the system disturbance is defined as follow (Fig. 8) :
| (29) |
Using the physical parameters of controlled plant, the controllers are designed, and the calculated gains are presented in Table 3.
In the physical parameters of DUAV system, m=2.39 kg. And, the low pass filter is chosen as 1/(s+1). The initial values of states for simulation are defined as follows :
| (30) |
And, the altitude reference signal which is a trapezoid steps signal for evaluating the control performances is defined as Eq. (31).
| (31) |
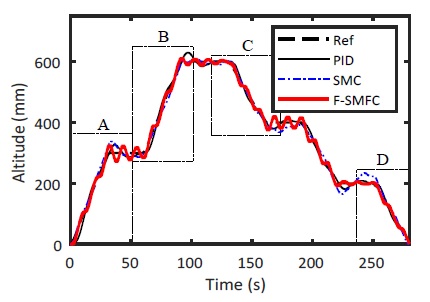
At first, the altitude tracking performances for the desired trapezoid steps signal are shown in Fig. 9 and Fig. 10. In this correspondence, all of the controllers (PID, SMC and F-SMFC) show good tracking performance.
In detail, as illustrated in Fig. 10 (A, B, C and D), the proposed F-SMFC method made the quickest responses for ascending and descending trajectory. In simulation process, the evaluation results of RMSE are summarized in Table 4.
Additionally, Fig. 11 and Fig. 12 draw the behavior of the tracking dynamic error of the DUAV system under control.
Evidently, the proposed F-SMFC method makes less RMS error than that of other methods.
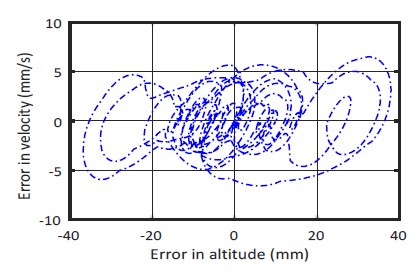
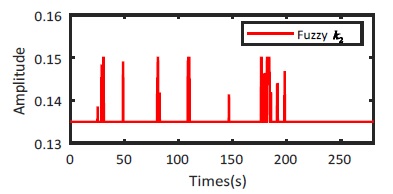
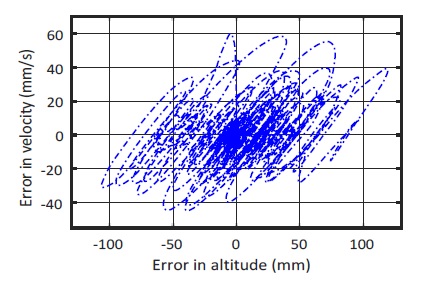
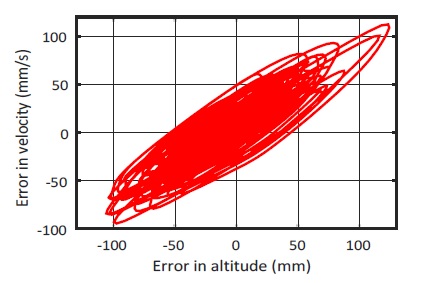
Something enhanced control performance of the proposed control is verified by the behavior of the output variable k2 and δ2 by using fuzzy law as shown in Fig. 13 and Fig. 14. Fig. 15 and Fig. 16 show the phase portrait characteristic of the SMC and F-SMFC method. The phase portrait of F-SMFC is either more stable node or stable focus than conventional SMC. Moreover, the stability of the DUAV system oscillates small range altitude error and quickly slides to equilibrium point.
Moreover, the stability of the DUAV system oscillates small range altitude error and quickly slides to equilibrium point.
5. Experiment studies
The result of the mathematical simulation and the mathematical model acquired using parameter identification has been presented in the last chapter. Based on these results, the motion control performance evaluations by experiment are shown in Figs. 17~26.
The specification of experimental apparatus and photo of controlled plant are illustrated in Table 5 and Fig. 17, respectively. In this system, the main propulsion system (BLDC motor) is provided to make driving forces for the DUAV system.
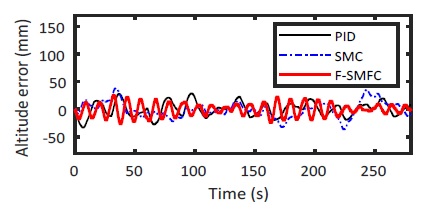
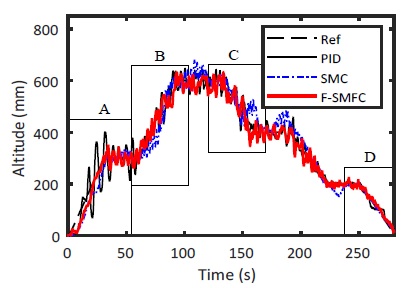
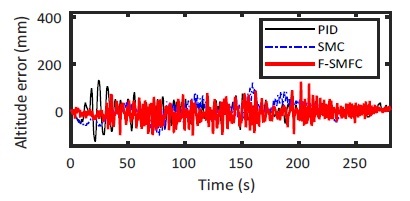
The control algorithms are employed on Labview software. The altitude position is measured by laser sensor. Fig. 18 and Fig. 19 show the effectiveness and satisfactory performances of the dynamic tracking altitude performance based on the designed controller. Similarly, all of the controllers (PID, SMC and F-SMFC) work well and effective with enhanced tracking performances (see Fig. 18). However, the proposed F-SMFC method preserves more stable and better tracking response than the other control methods.
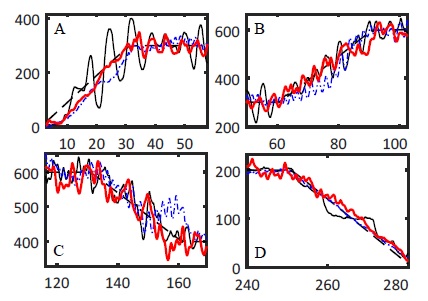
As illustrated in Fig. 19(A, B, C and D), the PID and SMC control made more oscillatory responses than the proposed method.
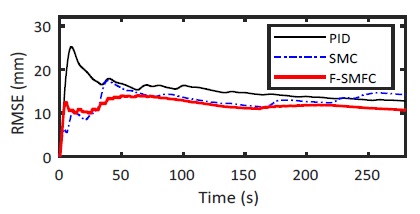
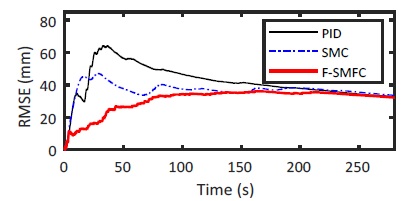
Fig. 20 and Fig. 21 draw the behavior of the tracking performance errors. Obviously, the proposed F-SMFC method presents less RMS error.
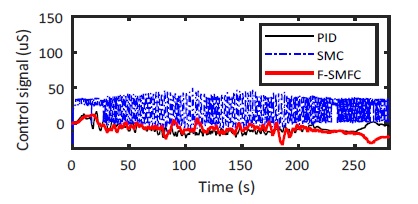
Fig. 22 illustrates the real control signals applied to the plant in experiment. The chattering phenomenon is well known and unavoidable characteristic of the SMC method.
Evidently, the proposed control method can suppress the undesirable oscillatory control signal such that it governs the chattering phenomenon and state reaches to the equilibrium point in short time.
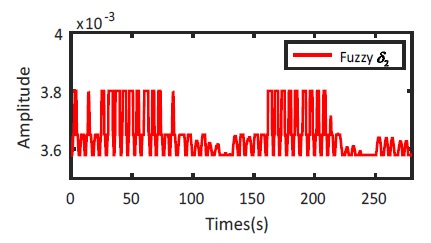
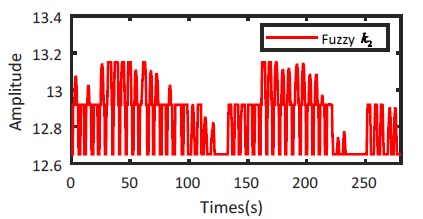
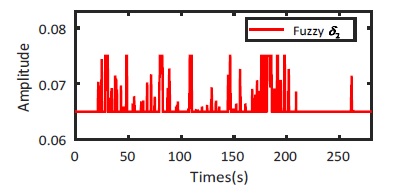
Similar to the simulation results, the efficiency of F-SMFC experimental method is also verified by the behavior of the output variable k2 and δ2 by using fuzzy law shown on Fig. 23 and Fig. 24, respectively.
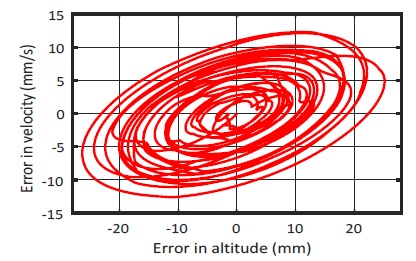
Besides, Fig. 25 and Fig. 26 show the phase portrait of the SMC and F-SMFC method in experiment implement. The phase portrait (F-SMFC) presents either more stable node or stable focus than the conventional SMC.
Evidently, from the phase portraits shown in Fig. 25 and Fig. 26, the stability of the DUAV system shows the similar altitude range error and rapid approaching to the equilibrium point.
6. Conclusions
In this study, a DUAV (ducted-fan unmanned aerial vehicle) control system design method is presented. The controlled plant consists of single propulsion system and several rudders.
The altitude position in cases of landing down and taking off is controlled by controlling propulsion force and rudder angles simultaneously. Due to the several reasons, the landing down process is operated in manual. It is the key motivation to provide a novel control strategy in this study. For this, this article proposes a new approach of sliding mode control (SMC) method by combining the fuzzy-sliding mode-feedback control (F-SMFC).
It gives the solutions of the problems such as governing the chattering phenomenon and arbitrarily exploiting the numeric control by the fuzzy law. And F-SMFC method could cope with the unknown physical parameter of the system.
Both simulation and experimental results were demonstrated to validate effectiveness and satisfactory performances of the proposed controller.
Author contributions
Y. B. Kim; Conceptualization. M. T. Tran; Data curation. H. C. Park; Formal analysis. H. C. Park; Funding acquisition. M. T. Tran; Investigation. Y. B. Kim; Methodology. Y. B. Kim; Project administration. D. H. Lee; Software. Y. B. Kim; Supervision. D. H. Lee; Validation. M. T. Tran; Writing-original draft. H. C. Park; Writing-original draft. D. H. Lee; Writing-review & editing.
References
-
W. Fan, C. Xiang, and B. Xu, 2018, "Modelling, Attitude Controller Design and Flight Experiments of a Novel Micro-Ducted- Fan Aircraft", Advances in Mechanical Engineering, Vol. 10, No. 3, pp. 1-16.
[https://doi.org/10.1177/1687814018765569]

-
A. Humaidi and A. Hasan, 2019, "Particle Swarm Optimization-Based Adaptive Super- Twisting Sliding Mode Control Design for 2-Degree-of-Freedom Helicopter", Measurement and Control, Vol. 52, No. 9-10, pp. 1403-1419.
[https://doi.org/10.1177/0020294019866863]

-
P. Martin and E. Salaun, 2010, "The True Role of Accelerometer Feedback in Quadrotor Control", Proc. of 2010 IEEE International Conference on Robotics and Automation, USA, pp. 1623-1629.
[https://doi.org/10.1109/ROBOT.2010.5509980]

-
M. D. Hua, T. Hamel, P. Morin, and C. Samson, 2013, "Introduction to Feedback Control of Underactuated VTOL Vehicles: A Review of Basic Control Design Ideas and Principles", IEEE Control Systems Magazine, Vol. 33, No. 1, pp. 61-75.
[https://doi.org/10.1109/MCS.2012.2225931]

- A. Intwala and Y. Parikh, 2015, "A Review on Vertical Take-Off and Landing (VTOL) Vehicles", International Journal of Innovative Research in Advanced Engineering, Vol. 2, No. 2, pp. 186-191.
-
R. F. Stengel, 2004, "Flight Dynamics", Princeton University Press.
[https://doi.org/10.1515/9781400866816]

- M. V. Cook, 2007, "Flight Dynamics Principles", Elsevier Ltd.
- P. Gelhausen and D. Enns, 2003, "Improving Control System Effectiveness for Ducted Fan VTOL UAVs Operating in Crosswinds", Proc. of 2nd AIAA "Unmanned Unlimited" Systems, Technologies, and Operations-Aerospace, America, pp. 2-11.
-
W. Zhengjie, L. Zhijun, F. Ningjun, and G. Meifang, 2013, "Flight Dynamics Modeling of a Small Ducted Fan Aerial Vehicle Based on Parameter Identification", Chinese Journal of Aeronautics, Vol. 26, No. 6, pp. 1439 -1448.
[https://doi.org/10.1016/j.cja.2013.10.006]

- M. T. Tran, D. H. Lee, S. W Ji, J. H. Suh, and Y. B. Kim, 2020, "A Study on the Dynamic Characteristics of Duct-Fan Type Propulsion System", Proc. of The Korean Society for Power System Engineering 2020 Spring Conference.
- A. Ko, O. J. Ohanian and P. Gelhausen, 2007, "Ducted Fan UAV Modeling and Simulation in Preliminary Design", AIAA Modeling and Simulation Technologies Conference and Exhibit, America, pp. 1-20.
-
M. Muehlebach and R. D'Andrea, 2017, "The Flying Platform : A Testbed for Ducted Fan Actuation and Control Design", Mechatronics, Vol. 2017, No. 42, pp. 52-68.
[https://doi.org/10.1016/j.mechatronics.2017.01.001]

-
Z. Omar, C. Bil and R. Hill, 2007, "The Application of Fuzzy Logic on Transition Manoeuvre Control of a New Ducted-Fan VTOL UAV Configuration", Proc. of IEEESecond International Conference on Innovative Computing, Information and Control, Japan.
[https://doi.org/10.1109/ICICIC.2007.562]

-
R. Naldi, L. Gentili, L. Marconi and A. Sala, 2010, "Design and Experimental Validation of a Nonlinear Control Law for a Ducted-Fan Miniature Aerial Vehicle", Control Engineering Practice, Vol. 2010, No. 18, pp. 747-760.
[https://doi.org/10.1016/j.conengprac.2010.02.007]

-
C. Edwards and S. K. Spurgeon, 1998, "Sliding Mode Control Theory and Applications", T. J. International Ltd, Padstow, UK.
[https://doi.org/10.1201/9781498701822]

-
S. K. Spurgeon, 2008, "Sliding Mode Observers : A Survey", International Journal of System Science, Vol. 39, No. 8, pp. 751-764.
[https://doi.org/10.1080/00207720701847638]

-
L. Fridman, J. Moreno and R. Iriarte, 2011, "Sliding Modes after the First Decade of the 21st Century", Springer.
[https://doi.org/10.1007/978-3-642-22164-4]

-
M. T. Tran, K. H. Kim, H. C. Park and Y. B. Kim, 2020, "A Study on an Adaptive Super-Twisting Sliding Mode Control Design with Perturbation Estimation", Journal of Power System Engineering, Vol. 24, No. 2, pp. 53-63.
[https://doi.org/10.9726/kspse.2020.24.2.053]

- P. M. Meshram and R. G. A. Kanojiya, 2012, "Tuning of PID Controller Using Ziegler- Nichols Method for Speed Control of DC Motor", Proc. of IEEE-International Conference On Advances In Engineering, Science And Management, India, pp. 117-122.
- C. F. Lin, T. J. Yu and X. Feng, 1996, "Fuzzy Control of a Nonlinear Pointing Tested with Backlash and Friction", Proc. of the 35th Conference on Decision and Control, Japan, pp. 4363-4368.