Evaluation of the Stress-Strain of Single-Layer Graphene Sheet Including a Crack
Abstract
Graphene is extremely thin, which exhibits extraordinary mechanical, physical and electrical properties, such that there are applications for this material in batteries and flexible displays. However, during the fabrication of commercial graphene devices, defects such as impurities and vacancies inevitably occur and the resulting cracks or notches can deteriorate the performance of graphene-based structures. Thus, it is necessary to understand the mechanical properties of graphene sheets including cracks so as to design healthy graphene-based structures. The present study investigated the effects of cracks (at various positions, distances and angles) on the strength of graphene. Four initial positions were considered in conjunction with uniaxial tensile loading, along with nine different distances and three initial angles. It was found that a crack located at the top center of the sheet represents the most vulnerable stress point, while a crack located further than one quarter of the sheet from the loading point had the greatest effect on the stress. In addition, the maximum stress was obtained in conjunction with a crack inclined at 45° relative to the loading direction. These results are expected to assist in the future evaluation for the safety usage of graphene sheets.
Keywords:
Graphene, Stress-strain, Molecular dynamics, Crack1. Introduction
Graphene is a nanomaterial comprising carbon atoms in a very thin layer based on hexagonal arrangements of atoms. Despite its thinness that is easy to bend, it has excellent mechanical properties, such as high strength and elastic modulus. In addition, the electrical properties of this material are highly unique. Accordingly, many researches are underway with regard to applications in flexible displays, transparent electrodes, touch panels, smart wearable safety devices, et al.1-2) However, these characteristics have not been fully utilized, although various manufacturing methods have led to renewed interest in manufacturing and actual product applications. Therefore, it is necessary to develop the technology to fully implement the properties of graphene in actual products.
Graphene for the commercial purposes can be manufactured by mechanical methods and by chemical exfoliation, epitaxial growth and chemical vapor deposition. Among these, chemical vapor deposition is the most attention because it is suitable for the mass production of high quality graphene. However, these methods can induce the cracks during the manufacturing process. This phenomenon poses a serious risk for the use of graphene. Thus, researches concerning the mitigation of defects and cracks during the manufacturing process are required.3-5)
Won6) studied the electromechanical behavior of cracks and damage in graphene transferred to a polymeric substrate using atomic force microscopy. Kim7) proposed a method for determining the crack tip cohesion law associated with the growth of graphene cracks. Wang et al.8) evaluated the effect of defects on the fracture strength of graphene sheets. Zhang et al.9) investigated the failure of monolayer graphene including central cracks through molecular dynamics simulations. Although such studies have examined graphene cracking and fracture mechanics, they have not been able to discern variations in the stress behavior depending on the position and shape of the crack initiation. It is very important to consider variables such as crack initiation, spread, propagation, growth and direction. Nguyen et al.10) examined the breakdown of monolayer graphene in the form of arm-chair and zig-zag cracks. Park11) studied the characteristics of arm-chair and zig-zag cracks in graphene using electron scattering. However, they failed to evaluate the stress behaviors with regard to initial cracking variables.
The purpose of present study is the evaluation of the stress behavior of graphene with a crack using MD(Molecular Dynamics) simulations. This work investigated the effects of various cracks induced during the manufacturing process for the graphene quality and device safety. These calculations using MD were performed LAMMPS (Large-scale Atomic and Molecular Massively Parallel Simulator code), which is capable of the microscopic-scale analysis of molecules such as graphene. The behaviors of various crack states occuring randomly in graphene were assumed for various cracking scenarios which would be occurred in a single layer graphene. MD simulation is a useful analytical method for observing graphene changes at the atomic level and determining the dynamics between atoms. It can be used to realistically identify cracks in nanomaterials such as graphene that are difficult to assess through standard tensile tests. The results from this study could be applied to establish criteria for evaluating the effect of cracks on the graphene products.
2. Methodology
2.1 Molecular dynamics
Most nanomaterials, including graphene, have a large specific surface area. The phenomena occurring on the surface greatly affect physical properties, of materials. If the structure changes minutely on the surface, it is difficult to control the change of the physical properties. This limitation can be solved by using MD technique which solves the motion of molecules based on Newton's equations. It is the only way to analyze the dynamic properties of a non-equilibrium system. MD are calculated in conjunction with the following four aspects.
For interatomic potentials, the evolution of the static and dynamic properties of each atom over time is defined. In the present study, graphene was calculated using the AIREBO (Adaptive Intermolecular Reactive Empirical Bond Order) potential.13) AIREBO enables simulations of the formation and rupture of covalent bonds for various atoms. This potential also determines the onset of cracking and allows for the precise calculation of bond formation and rupture based on the equation (1).
| (1) |
where is the energy stored in the bonds between atoms, is the nonbonding interaction between atoms and is the torsional interaction between atoms. Using the AIREBO potential value, the interatomic, nonbonding and torsional interactions in graphene can be determined.
Next, the using algorithm with MD simulation in this study was CG (Conjugate Gradient) method. It is used to calculate the new direction of modified atoms perpendicular to the previous direction by combining the force gradient with data obtained from the prior iteration. The highly accurate results are obtained by minimizing numerical errors during prolonged iterative calculations of the trajectories of all atoms in the system.
In a periodic system, atoms can interact across boundaries and exit one end of the box which make atoms move and reenter the other end. Therefore, PBC (Periodic Boundary Conditions) were used.
Also, the ensemble concept is used to simulate the motion of atoms over time. Initially, random molecular positions or lattice structures can be created and random positions of atoms and molecules are often arranged in a lattice structure because of the high risk of overlapping molecules. Representative ensembles include NVE(Number of atoms(N), Volume(V), and Energy(E) are isolated from changes in the system), NVT(Number of atoms(N), Volume(V), and Temperature(T) are conserved in the system) and NPT(Number of atoms(N), Pressure(P), and Temperature(T) are conserved in the system). The present work employed the NVT ensemble, which is the only one that can be used for controlling temperature condition of atoms similar to general experiments or systems. And the NVT ensemble is also called a canonical ensemble.
2.2 Analytical model
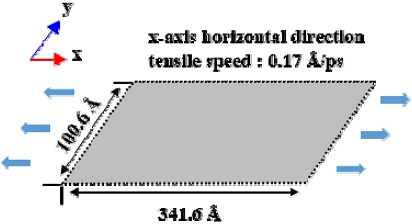
The graphene analytical model is illustrated n in Fig. 1. The horizontal and vertical dimensions of this model are 341.6 and 100.6 Å, respectively. The sample sheet was stretched at both ends in the x-axis direction, and the tensile velocity was set at 0.17 Å/ps.
The total number of atoms used to model the sample sheet was 13,296 and the conditions of molecular dynamic analysis applied to the graphene sheet are provided in Table 1.
The temperature was fixed at 300 K and was controlled using a Nose-Hoover thermostat which is an analytical method using in MD simulation to realize NVT ensemble as an actual experiment conditions. As for the potential, CH.AIREBO was used. CH.AIREBO is the potential to calculate the interactions between carbon atoms, specifying carbon atoms. The cut-off distance, which affects the calculations by specifying the distance between atoms, was set at 1.92 based on the typical range of 1.7–2.0 Å designated by the AIREBO, and because 1.92 was the most suitable value for use in the model. The CG algorithm was employed to minimize this distance. All calculations employed Newton's equations, with the units set to the metal options so that the stress values could be converted to units of GPa.
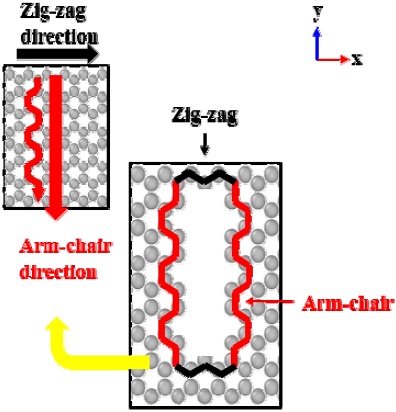
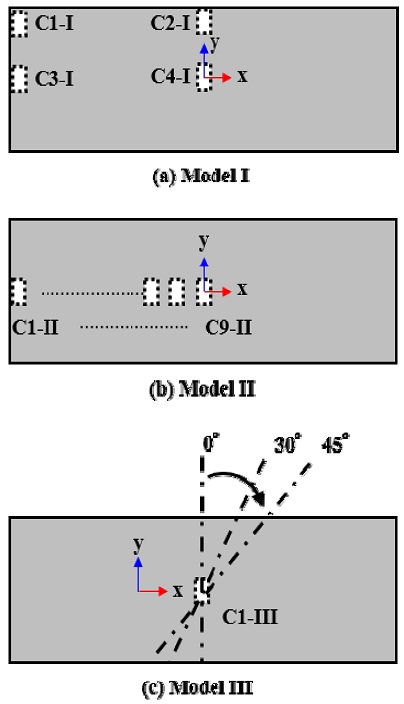
The initial shape of the crack inserted for the crack analysis was a combination of zig-zag and arm-chair morphologies with 18 atoms removed, as illustrated in Fig. 2. A total of three analytical models were employed, varying the positions, distances and angles at which these cracks were inserted, as presented in Fig. 3. Information regarding the position of the initial cracks is illustrated in Fig. 3. The analysis was performed for a graphene sheet divided into four parts symmetrically, so as to increase the efficiency of the analysis.
In Model Ⅰ, the graphene sample sheet was divided into four parts symmetrically and the crack was inserted at each of the four vertex positions as illustrated in Fig. 3 (a). Model Ⅱ analyzed nine cases with variations according to the x-axis relative to the center of the graphene sheet, as in Fig. 3(b). Finally, Model Ⅲ, as presented in Fig. 3(c), was divided into three cases of 0°, 30° and 45° in which the angle of the initial crack varied with respect to the load direction.
3. Results and discussion
3.1 The stress-strain curve according to the crack position
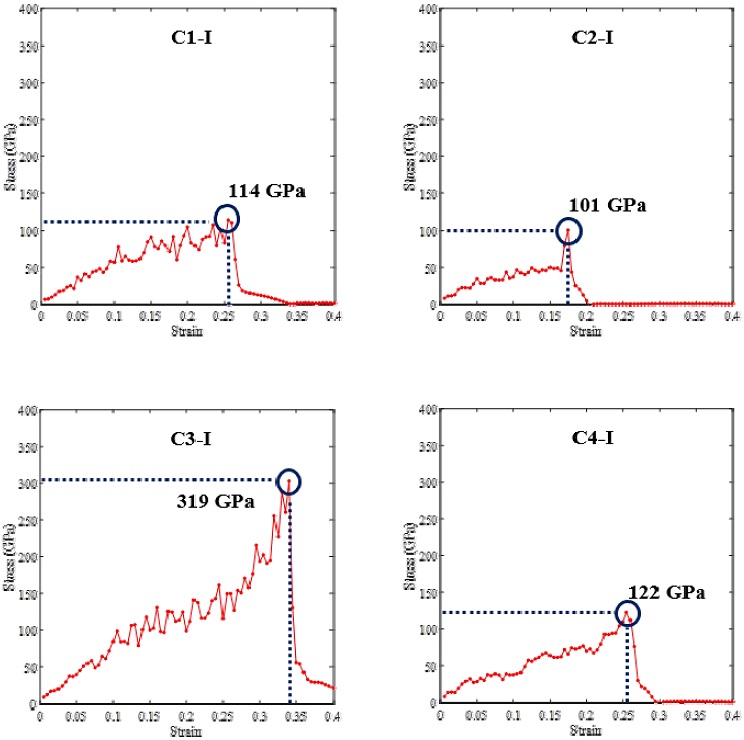
Stress-strain curves were obtained using the LAMMPS algorithm, and Fig. 4 shows the results of the analysis for the cracks at the four points of the graphene sheet in Model Ⅰ. In this model, the stress gradually increases to a maximum value in all of case after which it rapidly decreases. These maximum stresses indicate the failure strength. In addition, the graphene, which breaks immediately after reaching its failure strength without stress stagnation, evidently undergoes brittle fracture. Also the maximum stress value can indicate the initial cracking instability point in the graphene sheet. Consequently, a load should be applied below the maximum stress that the material can bear to prevent the failure of graphene due to cracking. In Model Ⅰ, the maximum stresses for the C1-Ⅰ, C2-Ⅰ and C4-Ⅰ cases were 114, 101 GPa, and 122 GPa respectively, while the C3-Ⅰ was 319 GPa. In the C3-Ⅰcrack of high stress 319 GPa, it is supposed the effect of saint-venant’s principle because of the localized stress concentration.
Fig. 5 shows the crack propagation leading to fracture. These images demonstrate two distinct patterns. One involves a single path which is divided two parts, as in the case of the C1-Ⅰ and C3-Ⅰ results, while the other is a dual path that divides into three parts, as in the C2-Ⅰ and C4-Ⅰ.
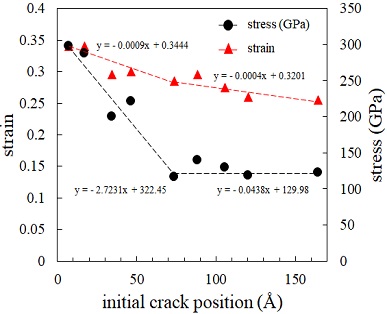
Next, a total of nine analyses were performed with Model Ⅱ, in which more initial cracks were inserted between the C3-Ⅰ and C4-Ⅰ distances used in Model Ⅰ, to determine the effect of the initial crack position in the center of the graphene sheet. The interval between these new distances was approximately 18 Å.
There maximum stress expresses the fracture strength. The both of stress and strain are decreasing according to the position of the initial crack tip. In particular, the decrease rate of the stress is faster than that of the strain, demonstrating that crack position affects highly the stress variation.
When the maximum stresses are compared with tensile strength of the smooth graphene sheet, the internal cracks have a great influence on the fracture strength. In Fig. 6, the variation of the maximum stress and strain have two phases that consist of two inclined lines. The values decrease swiftly until the position of about 90 Å from graphene sheet foundary. And after, it keeps stable stress value. However strains decrease slightly.
3.2 Stress variation according to the crack angle
The cracks generated in a structure do not always occur vertically or horizontally. Therefore, the effects of changes in the angle of the crack also need to be considered. The angular orientation of the initial crack was changed based on the length of the x-axis.
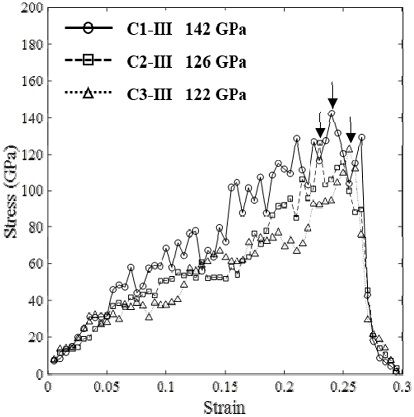
Fig. 7 shows the stress-strain curves obtained from the analysis of the C1-Ⅲ, C2-Ⅲ and C3-Ⅲ cases. The breaking strength for the C1-Ⅲ, with an initial crack angle of 0°, was 122 GPa, while those for the C2-Ⅲ, C3-Ⅲ with the initial crack inserted at 30° and 45°, were 126 GPa and 142 GPa. Thus, the breaking strength was increased due to angular orientation, indicating that the initial crack at 0° resulted in easier breaking of the material.
These results show that the initial crack at 45° is harder to fracture than that of at 0° and 30°. The results from Model Ⅲ evaluation express that the loading orientation for the graphene sheet with a crack need to be considered to avoid the vertical direction for the crack.
4. Conclusions
The purpose of this study was to distinguish differences in stress-strain relationships that occur with changes in the position of cracks in a graphene sheet. The following conclusions were obtained.
1) Effects of the initial crack position showed that a sudden failure occurred when the crack was located close to the central axis. And an initial crack in a single graphene sheet tends to advance to the fracture at the same time as growth starts, meaning that the graphene exhibits brittle fracture due to cracking.
2) In the analysis of the position of the initial crack by dividing the graphene sample sheet into four parts symmetrically(Model I), the upper center initial crack was the most vulnerable part with the fracture strength of 101 GPa. In addition, the propagation of fractures in graphene can follow two types of path shapes.
3) In the analysis of the position of the initial crack along the x-axis direction(C5-II), it was found that the a quarter part from the center initial crack was the most vulnerable part with the fracture strength of 116 GPa.
4) In the analysis of the angular orientation of the initial crack(Model III), the effects of the initial crack demonstrated that the 45° initial crack to the loading orientation was the highest fracture strength with a value of 142 GPa.
Acknowledgments
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education under grant number 2020R1F1A106863511.
Author contributions
O. H. Kwon; Conceptualization, Supervision and Writing-review & editing. W. R. Park; Project administration and Visualiztion. S. M. Kim; Investigation, Writing-original draft, Data curation and Visualiztion.
References
-
H. J. Lee, T. K. Choi, Y. B. Lee, H. R. Cho, R. Ghaffari, L. Wang, H. J. Choi, T. D. Chung, N. Lu, T. Hyeon, S. H. Choi and D. H. Kim, 2016, "A graphene-based electrochemical device with thermoresponsive microneedles for diabetes monitoring and therapy", Nature Nanotechnology, Vol. 11, No. 6, pp. 566-572.
[https://doi.org/10.1038/nnano.2016.38]

-
K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, 2004, "Electric field effect in atomically thin carbon films", Science, Vol. 306, No. 5696, pp. 666-669.
[https://doi.org/10.1126/science.1102896]

- S. Y. Choi, J. Y. Kim, H. K. Choi, J. H. Kim, C. G. Choi and T. Zyung, 2011, "Synthesis, properties and applications of graphene", Electronics and Telecommunications Trends, Vol. 26, No. 3, pp. 61-70.
- J. T. Han, H. J. Jeong, S. Y. Jeong and G. W. Lee, 2011, "Preparation of chemically exfoliated graphene nanosheets and its applications", Polymer Science and Technology, Vol. 22, No. 2, pp. 137-145.
-
K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J. H. Ahn, P. Kim, J. Y. Choi and B. Y. Hong, 2009, "Large-scale pattern growth of graphene films for stretchable transparent electrode", Nature, Vol. 457, No. 7230, pp. 706-710.
[https://doi.org/10.1038/nature07719]

- S. J. Won, 2015, "Electromechanical behavior of multilayer graphene on polymer substrate". Korea Advanced Institute of Science and Technology, PhD Thesis.
-
H. G. Kim, 2013, "Evaluation of crack-tip cohesive laws for the Mode I fracture of the graphene from molecular dynamics simulations", Computational Structural Engineering Institute of Korea, Vol. 26, No. 5, pp. 393-399.
[https://doi.org/10.7734/COSEIK.2013.26.5.393]

-
M. C. Wang, C. Yan, L. Ma, N. Hu and M. W. Chen, 2012, "Effect of defects on fracture strength of graphene sheets", Computational Materials Science, Vol. 54, pp. 236-239.
[https://doi.org/10.1016/j.commatsci.2011.10.032]

-
P. Zhang, L. Ma, F. Fan, Z. Zeng, C. Peng, P. E. Loya, Z. Liu, Y. Gong, J. Zhang, X. Zhang, P. M. Ajayan, T. Zhu and Jun Lou, 2014, "Fracture toughness of graphene", Nature Communications, Vol. 5, p. 3782.
[https://doi.org/10.1038/ncomms4782]

-
M. K. Nguyen and Y. J. Yum, 2014, "Mode Ⅲ fracture toughness of single layer graphene sheet using molecular mechanics", Transactions of the Korean Society of Mechanical Engineers, A, Vol. 38, No. 2, pp. 121-127.
[https://doi.org/10.3795/KSME-A.2014.38.2.121]

- C. W. Park, 2012, "Electron scattering and localized states at the graphene edge", Seoul National University, PhD Thesis.
-
S. J. Stuart, 2000, "A reactive potential for hydrocarbons with intermolecular interactions", The Journal of Chemical Physics, Vol. 112, No. 14, pp. 6472-6486.
[https://doi.org/10.1063/1.481208]