A Study on an Adaptive Super-Twisting Sliding Mode Control Design with Perturbation Estimation
Abstract
In this article, the adaptive super-twisting sliding mode control is designed and applied for three degrees of freedom robot with unknown perturbation model of the system. This method combines an advanced property of adaptive law and the high order super-twisting sliding mode control to enhance the sliding manifold surface which can reach the equilibrium point in the shorter time. Likewise, the stability and estimation of the unknown perturbations of the controlled system are satisfied by Lyapunov stability theory and Moreno's theorem. The effectiveness of adaptive super-twisting sliding mode control in unknown perturbation of the system is verified by comparing with the general super-twisting sliding mode control method. Therefore, a comparison results of both controllers via simulation are implemented. Also, the root mean square error is calculated for evaluation of the both controller's tracking performances.
Keywords:
Super-twisting, Adaption, Sliding mode control, Unknown perturbation, Lyapunov stability theory1. Introduction
The sliding mode controller (SMC) technology is perhaps originally a useful control method to deal with high nonlinearity and parameter fluctuations of the controlled system. This potential controller was evolved from pioneering working in the 1960s by Chrisstopher Edwards and Sarah K. Spurgeon.1) In the advanced SMC, the dynamic response of the system is suitably chosen of switching control function. However, the disadvantage of this technology has a fundamentally discontinuous control signal in the domain of control applications. To solve this issue, approximating or smoothing strategies is added to SMC implementation.
Many types of SMC methods have been reported, such as second order sliding mode algorithm, the sliding mode observer paradigm and a Lie-algebraic observer canonical form, etc. And, output feedback SMC, Sliding block control and discrete time sliding mode control, etc2,3) have given something desirable control performance. Furthermore, the super-twisting algorithm (STA) is the most advanced one of SMC methods presented in this time, which is widely applied and used to second-order sliding mode technique.4) STA provides a solution that considerably reduces the chattering phenomenon in control behavior. Notably, the super-twisting sliding mode control (STSMC) strategy is basically designed based on the Lyapunov theory to occupy the system stability.5) Therefore, the super-twisting SMC has the known properties of finite time convergence and robustness against internal and external uncertain dynamic characteristics.
Alexander Barth et al. designed a super-twisting sliding mode controller based on Lyapunov stability theory by using certainty equivalence principle.6) In this paper, the STSMC combined with the part of adaption law was considered on the single input and single output (SISO) system to relax the bounded condition and reduce the sliding mode gains significantly. Where, the system stability is guaranteed by Lyapunov theory. Jorge Davila et al. modified the super-twisting sliding mode technology with second order to design a velocity observer for uncertain mechanical systems.7) The discrete form of the observer is designed and implemented separately from the controller. Especially, a case study of discrete form of the observer was demonstrated to evaluate the effectiveness of this algorithm in experiment. Dimitrios Papageorgiou et al.8) estimated the robust backlash problem by using sliding mode and adaptive principles on industrial drive train systems. In this study, a super-twisting sliding mode observer was designed in order to estimate the injection signal. Likewise, the adaptive part was added into the observer to update the dead zone of backlash angle. The controller theories of dynamic system response and robustness were successfully validated by the experiments.
More specially, an optimal adaptive super-twisting sliding mode strategy was deployed for two-axis helicopter, which was done by Amjad J Humaidi et al..9) The proposed controller was developed based on STA method and Lyapunov theory to avoid the chattering phenomena and estimate the unknown parameters, respectively. The simulations for two-axis helicopter were demonstrated and the effectiveness of controller theory was verified too.
Besides, the adaptive control provides its advantages in the automatic adjustment of the controllers or guarantee the performance of the control system while the parameters of dynamic model parameters are unknown or perturbed in real time.10) Another area of current interest is the development of adaptive control with possibly unknown perturbations such as backlash, viscous friction and vibration, etc.11-16) An intense focus on one of the most advantages of the adaptive control is the global stability which is guaranteed by the Lynapunov theory. Hence, the adaptive law is easily combined with the other controllers such as sliding mode control, PID, backsteping, and fuzzy logic, etc. such that it becomes more advanced controller.
The motivation of this paper is to solve the unknown perturbation problems such as backlash, viscous friction and vibration, etc. for 3-DOF robot manipulator.
Throughout the some fundamentally different advantages and disadvantages of STSMC, an adaptive super-twisting sliding mode control (ASTSMC) will be deployed with 3-DOF system.
Then, the contributions of this paper are emphasized as follows:
■ Design of super-twisting sliding mode control for 3-DOF system in detail. ■ The stability analysis and definition of bound of unknown perturbation of system in STSMC based on Lyapunov theory and Moreno's theorem.■ Design of adaptive super-twisting sliding mode control for 3-DOF system in detail.■ A comparison with STSMC and ASTSMC has been implemented.
This paper is organized as follows. Section 2 discusses the modeling of the 3-DOF system with unknown parameters. Section 3 analytically describes the design of STSMC for the controlled system in detail and provides the convergence and stability condition of STSMC by Lyapunov theory and Moreno's theorem. The ASTSMC has been designed in detail in section 4, where also a proof for the global stability of unknown perturbations system is verified by Lyapunov theory. The simulation validation of the theoretical findings is presented in section 5. Section 6, conclusions will been drawn.
2. System Modeling Equation with Unknown Perturbations
An identification and tuning method of the system parameters with MATLAB/Simulink has been clearly illustrated.17) However, the identified and tuned parameters are generally considered as nominal and constant values for designing the controller. Notably, the nominal values are affected by the operating condition, external disturbance and uncertainties such as backlash, viscous frictions and etc. It is natural that we consider the unknown perturbations in control system design process.
Then, let us describe the dynamic equation of the controlled system. The general description for 3-DOF robot system with uncertainties is given as follows:
| (1) |
Where θi[deg] is the angular positions of the system. ui[V] is the control input signals of the each actuator. fi(t,ϕi) is the dumped unknown perturbations of the system such as backlash, viscous frictions etc.
Where, the nominal values of parameters given Eq. (1) are defined as follows:
a1 =350, a2 =2362, a3 =10310,
b1 =-16, b2 =-140, b3 =-143,
c1 =-0.008, b2 =-0.0001, b3 =-0.01.
[Remark 1] fi(t,ϕi) is the uncertain perturbations. The derivative of uncertainty satisfies , where δi(> 0) is the upper bounds of the derivative of the unknown perturbations.
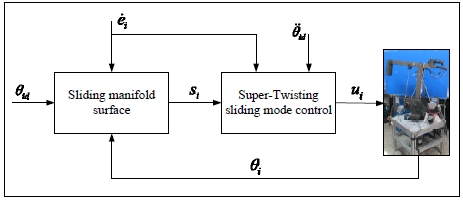
3. Super-Twisting Sliding Mode Control Design
The relation of the uncertain perturbation and super-twisting sliding mode control theory is demonstrated with Lyapunov theory.4) Based on this results, the authors design a control system for controlling 3-DOF robot motion by estimating the uncertain parameters on adaptive rule.
Then, let us assign the sliding manifold surface as follows:
| (2) |
Where mi is positive parameters. The error ei between the desired angular position θid and the actual angular position θi is defined as follow:
| (3) |
Taking the derivative time of Eq. (2) gives
| (4) |
From Eq. (1) and Eq. (4), the following Eq. (5) is obtained with a condition of sliding manifold defined as Eq. (6).
| (5) |
| (6) |
Then, the control law based on the Super-Twisting Algorithm is calculated as following.
| (7) |
Where
| (8) |
And, the function sgn( • ) or sign( • ) is defined as
| (9) |
Then, we need to verify the system stability condition with the control law Eq. (7).
By substituting Eq. (7) into Eq. (5), the equivalent sliding manifold is given as following.
| (10) |
Where, ki and hi are positive control coefficients.
Then, the authors propose a canditate of Lyapunov function as follows:
| (10) |
The time derivative along the above Lyapunov function is given as follows:
| (11) |
Substituting Eq. (7), Eq. (8) and Eq. (10) into Eq. (11), then the Eq. (11) can be written as a quadratic form [5]:
| (12) |
where,
| (13) |
Applying the result of Moreno and Osorio,18) the bounds of the perturbations are presented as follows:
| (14) |
where,
| (15) |
The expression for the derivative of the Lyapunov function Eq. (12) is reduced to
| (16) |
where
| (17) |
[Remark 2] The system stability is preserved, if the controller gains satisfy the following conditions:
| (18) |
then . This condition implies that Vi > 0 and for all the time t ≥ 0. This clearly indicates the sliding manifold (si) will converge to zero with t→∞. ▀
[Remark 3] The Moreno and Osorio’s result18) gives that the state of the system can reach the equilibrium point with t→∞ by STSMC. Then the convergence time is written as follows:
| (19) |
where,
| (20) |
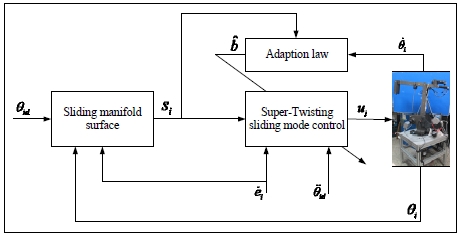
4. Adaptive Super-Twisting Sliding Mode Control Design
In the controlled systems, there are many uncertain parameters which may not be directly measured and estimated. Also, the considered robot system of this study has several uncertain parameters. As abovementioned, the target parameters to be estimated in this study are bi which are shown in Eq. (1) and Eq. (5).
It is well known fact that the super-twisting SMC cannot acquire the exact control law with uncertain parameters. Therefore, we need to estimate the uncertain parameters by adaptation method for applying the super-twisting SMC to this issue.
The adaption law is designed to update and estimate the real values bi. Then estimation errors with the estimated values are defined as
| (21) |
Using this relation, the controlled system shown in Eq. (1) can be rewritten
| (22) |
Then, the sliding manifold surface with adaptation rule is assigned as
| (23) |
Where ni is positive parameters, and ( · )*adap are the parameters being adapted. The error between the desired position θid and the actual position θi is defined
| (24) |
And, the time derivative of Eq. (23) is calculated as
| (25) |
The updated adaptive super-twisting sliding mode control law is assigned as
| (26) |
where,
| (27) |
with constant values μi > 0 and ηi > 0.
The following is the proof for verifying the system stability. Using the well known Lyapunov method, a Lyapunov candidate of the adaption manifold sliding surface yields
| (28) |
Then the time derivative the Lyapunov function Eq. (28) is
| (29) |
Substituting Eq. (26) into Eq. (22), we can obtain
| (30) |
The time derivative of the adaption sliding manifold surface Eq. (25) from Eq. (24) and Eq. (30) becomes
| (31) |
Taking Eq. (31) into Eq. (29), because of in the derivative time, the time derivative of the Lyapunov function becomes
| (32) |
[Remark 4] The stability of the system is preserved, if the controller gain and the term satisfy the adaption laws determined as follows:
| (33) |
This condition keeps Vi > 0 and for all the time. Therefore, the sliding manifold surface (si) and the estimation perturbation () will converge to zero with t→∞. ▀
5. Simulation results
Simulations were provided for demonstrating the convergence and accuracy properties of the proposed control scheme. The performance comparison study of the adaptive super-twisting SMC with the conventional super-twisting SMC method was performed and discussed through simulation.
5.1 Nominal case
Firstly, the simulated results were implemented by the nominal value (bi) from the identification algorithm. Where the nominal values of the parameters are b1 = -16, b2 = 140, b3 =-143 with the unknown parameter set as fi = 0.
Secondly, the another simulation considering perturbed values () by estimating was done to show better properties of ASTSMC than the non-adaptive control scheme with unknown perturbation terms.
The initial values including states and parameters for simulation were defined as following to initialize the simulation for both the adaptive and conventional super-twisting sliding mode control system.
| (34) |
The calculated controller gains for two control schemes are summarized in Table 1. As mentioned before, the robot system with three arms is controlled by three independent controllers. Then the controller gains for each arm are represented as Table 1.
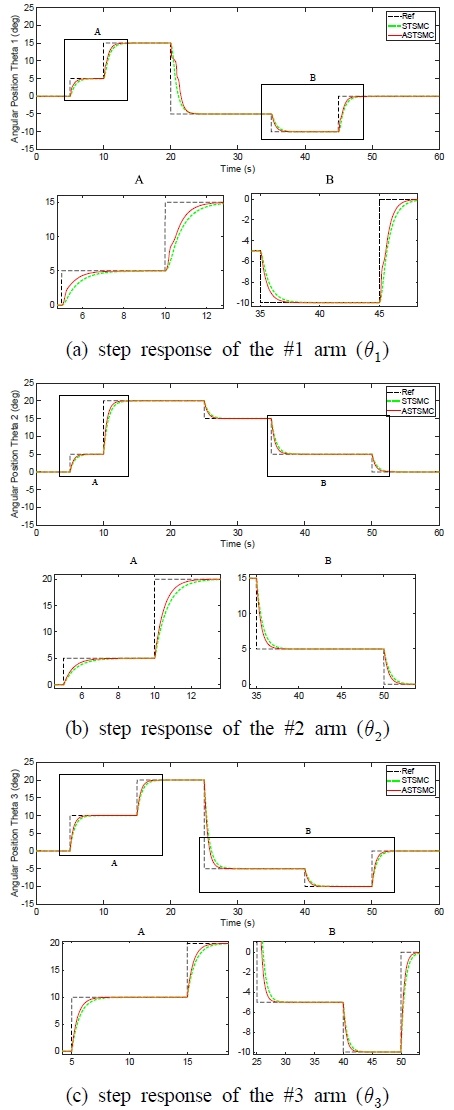
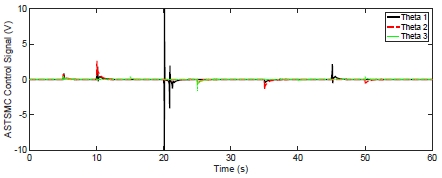
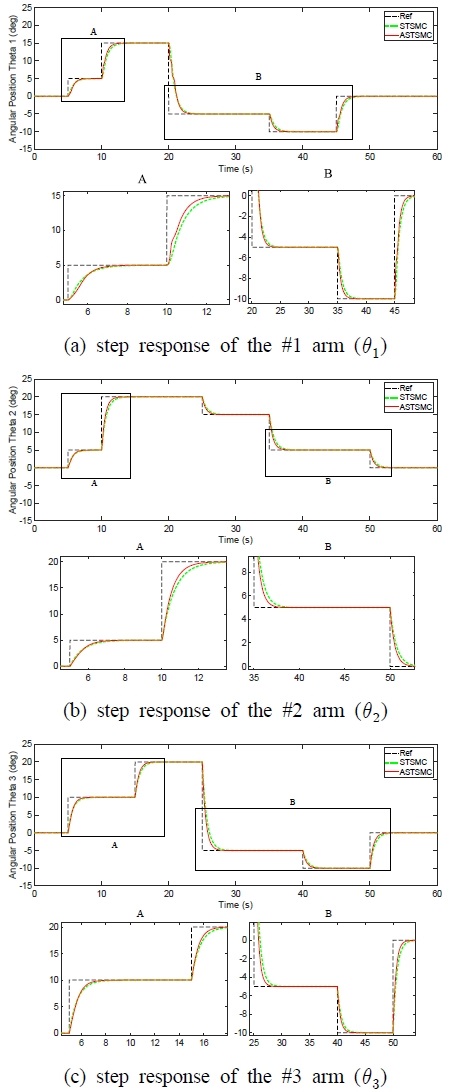
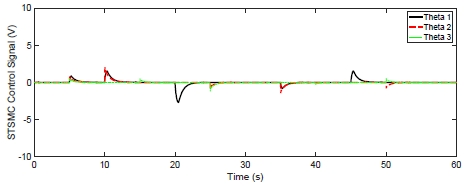
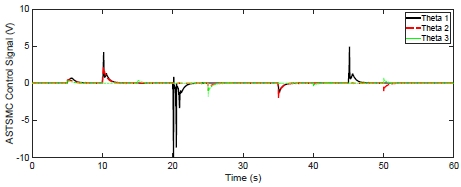
At first, the dynamic response of the ASTSMC and STSMC in nominal condition are shown in Fig. 3.
Fig. 3 shows the tracking responses of three arms’ angular positions (θ1,θ2,θ3) for the step type reference signal.
With the nominal values in which parameters bi are constant, we found that the control performance of ASTSMC is better than STSMC. As illustrated in ‘A’ and ‘B’ which are zoomed in on the each figure, the ASTSMC method can quickly update the unknown physical parameters of the system such that faster responses without overshoot are obtained than the conventional STSMC.
As similar to tracking performance comparison study, the errors of the angular positions θ1,θ2,θ3 were calculated and shown in Table 2. This result gives us same conclusion.
5.2 Perturbed case
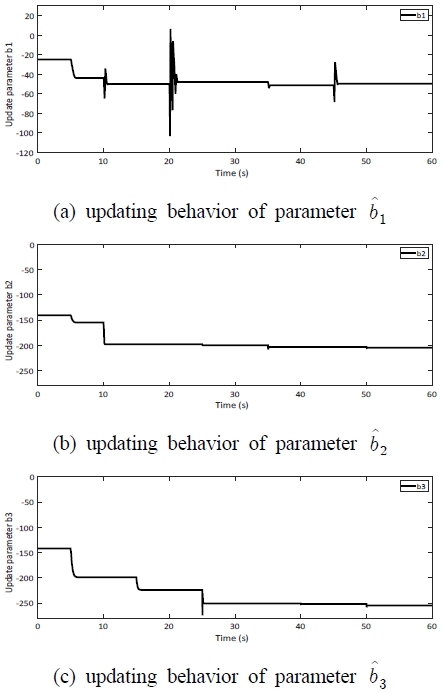
To make a clearer comparison in case of uncertain condition, the different parameters values were set. They were defined as b1 =-50, b2 =-200, b3 =-253 with the unknown parameter () perturbation rate fi = 15%. The effect of parameter perturbations on dynamic tracking response of the controlled system is shown from Fig. 6 ~ Fig. 9.
Fig. 6 shows the tracking responses of three arms’ angular positions (θ1,θ2,θ3) for step type reference signal. With the uncertain parameters bi, we found that the control performance of ASTSMC The errors of the angular position tracking were also evaluated. The evaluation result is summarized in Table 3. Evidently, the adaptive super-twisting sliding mode control made less RMS error than the conventional method. Finally, the behaviors of the design parameters concerning optimization process with ASTMSC are shown in Fig. 9.
5. Conclusions
In this study, the adaptive super-twisting sliding mode control strategy was developed and applied to 3DOF robot motion control problem with unknown parameters estimation including nominal case.
The advanced properties of this technology was demonstrated by combing conventional high order sliding mode control and adaptive control theory. The system stability, convergency of states by Lyanpunov method and controller gains estimation are definitely guaranteed.
From the two simulation studies, we found that the ASTSMC method could cope with the parameter uncertainty such that it can keep better control performance and robustness than conventional sliding mode control method.
Most physical systems have dynamic parameters which are time varying. Therefore it is natural that we provide a real time parameter updating strategy. The adaptive sliding mode control method is a solution for this issue.
Finally, we can conclude that the proposed ASTSMC guarantees better tracking performance and stronger robustness to the uncertain dynamics.
References
-
C. Edwards and S. K. Spurgeon, 1998, "Sliding mode control theory and applications", T. J. International Ltd, Padstow, UK. (ISBN: 9780748406012)
[https://doi.org/10.1201/9781498701822]

-
S. K. Spurgeon, 2008, "Sliding mode observers: a Survey", International Journal of System Science, Vol. 39, No. 8, pp. 751-764.
[https://doi.org/10.1080/00207720701847638]

-
L. Fridman, J. Moreno and R. Iriarte, 2011, "Sliding modes after the first decade of the 21st century", Springer.
[https://doi.org/10.1007/978-3-642-22164-4]

- J. Rivera1, L. Garcia, C. Mora, J. J. Raygoza and S. Ortega, 2011, Sliding mode control, InTech, India. (ISBN: 978-953-307-162-6)
-
A. Bacciotti and L. Rosier, 2005, "Liapunov functions and stability in control theory", Springer. (ISBN: 978-3-540-21332-1)
[https://doi.org/10.1007/b139028]

-
A. Barth, M. Reichhartinger, J. Reger, M. Horn and K. Wulff, 2015, "Lyapunov-design for a super-twisting sliding-mode controller using the certainty-equivalence principle", International Federation of Automatic Control, Vol. 2015, No. 48-11, pp. 860-865.
[https://doi.org/10.1016/j.ifacol.2015.09.298]

-
J. Davila, L. Fridman, and A. Levant, 2005, "Second-order sliding-mode observer for mechanical systems", IEEE Transactions on Automatic Control, Vol. 50, No. 11, pp. 1785-1789.
[https://doi.org/10.1109/TAC.2005.858636]

-
D. Papageorgiou, M. Blanke, H. H. Niemann and J. H. Richter, 2019, "Robust backlash estimation for industrial drive-train systems theory and validation", IEEE Transactions on Control Systems Technology, Vol. 27, No. 5, pp. 1847-1861.
[https://doi.org/10.1109/TCST.2018.2837642]

-
A. J. Humaidi and A. F. Hasan, 2019, "Particle swarm optimization-based adaptive super-twisting sliding mode control design for 2-degree-of- freedom helicopter", Measurement and Control, Vol. 52(9-10), pp. 1403-11419.
[https://doi.org/10.1177/0020294019866863]

-
I. D. Landau, R. Lozano and M. M'Saad, 1998, "Introduction to adaptive control", Springer.
[https://doi.org/10.1007/978-0-85729-343-5_1]

-
J. Huang, C. Li, and B. Y. Duan, 2010, "Adaptive backstepping integral control of servo systems with backlash", Journal Systems and Control Engineering, Vol. 225, No. IMechE, pp. 1149-1162.
[https://doi.org/10.1177/0959651811400950]

-
G. Tao and P. V. Kokotovic, 1995, "Adaptive control of systems with unknown output backlash", IEEE Transactions on Automatic Control, Vol. 40, No. 2, pp. 326-330.
[https://doi.org/10.1109/9.341803]

-
G. Tao and P. V. Kokotovic, 1993, "Adaptive control of systems with backlash", Automatica, Vol. 29, No. 2, pp. 323-335.
[https://doi.org/10.1016/0005-1098(93)90126-E]

- C. F. Lin, T. J. Yu and X. Feng, 1996, "Fuzzy control of a nonlinear pointing testbed with backlash and friction", Proc. 35th Conference on Decision and Control, Japan, pp. 4363-4368.
-
G. Chen, W. Zhang, X. Li and B. Yu, 2019, "Adaptive speed control method for electromagnetic direct drive vehicle robot driver based on fuzzy logic", Measurement and Control, Vol. 52(9-10), pp. 1344-1353.
[https://doi.org/10.1177/0020294019866841]

-
S. A. Abhari, F. Hashemzadeh, M. Baradarannia and H. Kharrati, 2019, "An adaptive robust control scheme for robot manipulators with unknown backlash nonlinearity in Gears", Transactions of the Institute of Measurement and Control, Vol. 41, No. 10, pp. 2789-2802.
[https://doi.org/10.1177/0142331218810773]

- M. S. Tran, E. H. Choi and Y. B. Kim, 2017, "A study on response time delay and tracking error suppression strategy in gear mechanism : Control system design approach", Journal of the Korean Society for Power System Engineering, Vol. 21, No. 4, pp. 77-83.
-
J. A. Moreno and M. Osorio, 2008, "A Lyapunov approach to second-order sliding mode controllers and observers", Proc. 47th IEEE Conference on Decision and Control, Mexico, pp. 2856-2861.
[https://doi.org/10.1109/CDC.2008.4739356]

M. T. Tran; Conceptualization, Formal analysis, Methodology and Writing-review & editing. K. H. Kim and H. C. Park; Validation & editing. Y. B. Kim; Writing-original draft, Project adminstration and Supervision.